Языки: Maple, Фортран
Программа предназначена для построения d-мерных квадратурных формул порядка p в развернутом виде для интегрирования по d-мерному стандартному единичному
симплексу Δd
с вершинами 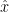 j
= (
j
= (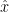 j1
,...,
j1
,..., 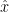 jd
),
jd
), 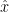 jk
= δjk
, j=0,...d, k=1,...d,
jk
= δjk
, j=0,...d, k=1,...d,
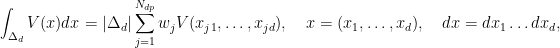
точное для всех многочленов от переменных
x1,...,xd
степени, не превышающей
p, где
|Δd| = 1/d! — объем симплекса.
Здесь
Ndp — количество узлов,
wj — веса,
(xj1,...,xjd) — узлы.
Подробное описание метода построения полностью симметричных квадратурных формул с положительными весами и с точками, лежащими в 2-,...,6-симплексе (т.н. PI-типа), представлено в [1].
Файлы *.mw и *.f содержат программы на языках Maple и Фортран для преобразования квадратурных формул до 20-го порядка на треугольнике и тетраэдре, 16-го порядка на 4-симплексе, 10-го порядка на 5- и 6-симплексы в развернутом виде и примеры их применения:
- • INPUT:
- ○ файл `ddxoy_z.dat',
- • OUTPUT:
- ○ wg - массив весов размерностью gnodes,
- ○ xg — массив барицентрических координат узлов размерностью (dim+1)*gnodes.
Файлы `ddxoy_z.dat' содержат размерность симплекса, порядок квадратурной формулы, количество узлов, информацию об орбитах и полностью симметричные квадратурные формулы PI типа в барицентрических координатах
(y1,...,yd+1) в компактной форме, где
- • x=dim означает размерность симплекса,
- • y=p означает порядок квадратурной формулы,
- • z=gnodes означает количество узлов.
В качестве примера рассмотрены интегралы
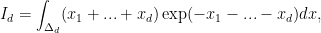
которые вычисляются аналитически и при
d=2,...,6 равны:
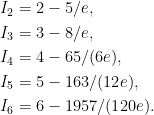
Отметим, что полученные барицентрические координаты узлов
(yj1,...,yjd+1) можно использовать для интегрирования по
d-мерному произвольному симплексу
Δq
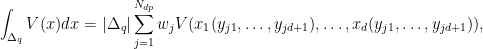
при этом объём симплекса
|Δq| должен быть вычислен отдельно.
Скачать архив программы INQSIM.
Литература:
- G.Chuluunbaatar, O.Chuluunbaatar, A.A.Gusev, an S.I.Vinitsky.
PI-type fully symmetric quadrature rules on the 3-,...,6-simplexes.
Computers & Mathematics with Applications, 124, 89--97 (2022).




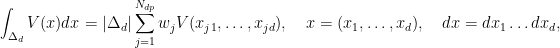
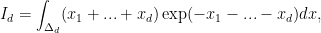
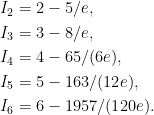
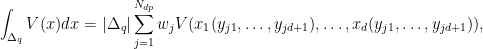





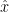 j
= (
j
= (