|
|
|

|
БИБЛИОТЕКА ПРОГРАММ JINRLIBRK4-MPI - параллельная реализация численного решения задачи Коши |
|
|
|
|
Язык: C++ Программа RK4-MPI предназначена для параллельного численного решения задачи Коши в форме 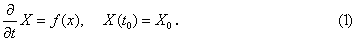 Здесь Х – вектор-столбец неизвестных, состоящий из последовательно расположенных L блоков длины M. Функция f такова, что для каждого i-го уравнения системы она зависит от локально расположенных элементов вектора Х с номерами i, i+1, i-1. Подобные задачи часто возникают при аппроксимации уравнений в частных производных с помощью конечно-разностных формул. Указанная структура функции f позволяет организовать параллельную реализацию расчета по формуле Рунге – Кутты на основе распределения L блоков между NP параллельными MPI-процессами таким образом, что обмен происходит лишь между процессами с отличающимися на 1 номерами, обрабатывающими соседние сегменты массива Х, для взаимной пересылки граничных элементов этих сегментов. Подобная схема параллельной реализации метода Рунге – Кутты использовалась, например, в работе [1] для численного исследования сверхпроводящих процессов в системе длинных джозефсоновских переходов, а также в работе [2] для компьютерного моделирования прохождения многокомпонентной газоконденсатной смеси через пористую среду. Расчеты показывают уменьшение времени счета при запуске в параллельном режиме в 5-10 раз (в зависимости от размерности задачи и количества задействованных параллельных процессов) по сравнению с последовательным расчетом на одном узле. Программа RK4-MPI вычисляет один шаг интегрирования системы (1) по формуле Рунге – Кутты четвертого порядка [3] с помощью функции RK4. В функции RK4 при заданном начальном значении t=t0 и заданном начальном состоянии Х=X0 каждый из задействованных NP процессов вычисляет значения назначенных ему к расчету элементов массива Х для t=t0+ht. Функция ff вызывается из RK4 для организации обмена граничными данными между процессами. Строка для вызова функции RK4 имеет вид: Входные параметры:
♦ f - функция, которая составляется пользователем для вычисления правой части системы (1);
♦ g - составляемая пользователем функция для сборки распределенных по процессам блоков массива Х в один массив процесса с номером 0 и сохранения результатов при текущем значении переменной t; ♦ M - размер каждого из L последовательно расположенных блоков в составе массива Х (общая длина массива неизвестных – L*M); ♦ t и ht - начальное значение переменной t и шаг интегрирования по t (размер шага интегрирования определяется особенностями конкретной задачи, в том числе, при решении сеточных аналогов уравнений в частных производных необходимо учитывать соответствующее условие Куранта); ♦ m0 - номер первого М-элементного блока в назначаемом каждому процессу сегменте в глобальной нумерации блоков; ♦ m1, m2 - номера первого и последнего блока массива Х в каждом процессе; ♦ X - фрагмент массива неизвестных, состоящий в каждом процессе из последовательно расположенных блоков длины М с номерами от m1 до m2 и содержащих входные значения X0 соответствующих элементов Х; ♦ Y - фрагмент массива неизвестных, содержащий в каждом процессе результаты интегрирования при t+ht. Массив Y может совпадать с Х. В функциях f( t, m0, m1, m2, * Х, * dx) и g(t, m0, m1, m2, * Х, * dx) параметры t, m0, m1, m2, Х имеют такой же смысл, как и в процедуре RK4; dx – массив, содержащий сегмент производных по времени, вычисляемый каждым процессом. В программу пользователя должны быть включены строки:
#include "mpi.h"
#include "RK4.cpp" Программа пользователя должна быть оформлена согласно требованиям стандарта MPI. В ней должны быть вызваны MPI-функции, возвращающие номер MPI-процесса в группе и общее количество процессов. Например, так:
...
int main() {
int argc = 0; char **argv = NULL;
...MPI_Init(&argc, &argv); MPI_Comm_size( comm, &NP ); //NP - количество процессов MPI_Comm_rank( comm, &IP ); //IP - номер каждого процесса MPI_Finalize(); ... } Кроме того, пользователь должен перед вызовом функции RK4 организовать расчет значений m0,m1,m2, как это сделано в примере RK4test.cpp (cм. блок «Разметка MPI-процессов»). Тестовый пример реализует применение численного метода Рунге - Кутты для решения задачи теплопроводности на двумерной сетке по пространственным координатам, которая позволяет продемонстрировать распределение большого объема вычислений между процессами. Описание исходной постановки задачи, конечно-разностная система уравнений и особенности применения функции RK4 для ее решения представлены в файле description.pdf. Файлы RK4test.cpp, RK4test.par, RK4test.out содержат соответственно код, входные данные и результаты расчета. В качестве входных данных в RK4test.par задаются L и M - количество и размер блоков в составе массива Х, n - количество шагов интегрирования, ht - шаг интегрирования. Архив программы содержит:
1. Файл RK4.cpp (функции RK4 и ff)
2. Тестовая программа RK4test.cpp 3. RK4test.par - файл с входными параметрами 4. RK4test.out - файл с результатами расчета 5. test_description.pdf - описание тестовой задачи и структуры тестовой программы Скачать архив программы RK4-MPI. Литература:



|
|

