Язык: C++
Комплекс программ SPIN-Ga/Gr реализует построение доменов переворота магнитного момента
в модели φ0-джозефсоновского перехода на плоскости параметров модели. Динамика намагниченности в рассматриваемой модели описывается уравнением:
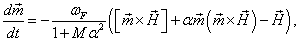 (1)
(1)
где α – параметр диссипации, ωF – нормализованная частота ферромагнитного резонанса. Здесь 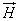 – эффективное магнитное поле по компонентам:
– эффективное магнитное поле по компонентам:
 (2)
(2)
где G – отношение джозефсоновской энергии к энергии магнитной анизотропии,
r – параметр спин-орбитальной связи,
mx,y,z – соответственно
x,y,z – компоненты магнитного момента 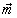 . Начальные условия:
mx(0) = 0, my(0) = 0, mz(0) = 1.
Джозефсоновская разность фаз φ(t) вычисляется через уравнение
. Начальные условия:
mx(0) = 0, my(0) = 0, mz(0) = 1.
Джозефсоновская разность фаз φ(t) вычисляется через уравнение
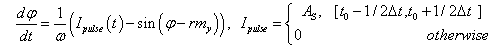 (3)
(3)
Здесь Ipulse – импульс тока, As – амплитуда импульса тока,
и Δt – временной интервал воздействия импульса тока, t0 – время максимальной амплитуды.
В представленных программах численное решение начальной задачи (1-3)
для системы обыкновенных дифференциальных уравнений реализовано
как на основе явного 4-шагового метода Рунге – Кутты,
так и с помощью неявной схемы Рунге – Кутты, называемой также методом Гаусса – Лежандра.
При этом расчет проводится на плоскости параметров
(G, α) или (G, r), где параметры G, α или G, r
меняются в заданном диапазоне с определенным шагом. В ходе вычислений для каждой пары
значений параметров на сканируемой плоскости идентифицируется переворот магнитного момента
(если начальное значение mz(0) = +1 в ходе моделирования меняет знак
и принимает значение mz(t) = –1) либо отсутствие переворота (сохраняется знак
z - компоненты магнитного момента mz(t) = +1).
Детальное изложение математической постановки задачи, вычислительной схемы и алгоритма идентификации переворота магнитного момента представлено в работе [1]. Схема параллельной реализации и результаты расчетов ускорения в зависимости от количества MPI-процессов и OpenMP-потоков, представлены в работе [2].
В комплекс SPIN-Ga/Gr включены по четыре версии программ для каждого из двух случаев: (1) расчет на плоскости (G, α) и (2) на плоскости (G, r), а именно:
• параллельная MPI-версия с реализацией решения задачи (1-3) методом Рунге – Кутты 4 порядка,
• параллельная MPI-версия с реализацией решения задачи (1-3) методом Гаусса – Лежандра,
• параллельная OpenMP-версия с реализацией решения задачи (1-3) методом Рунге – Кутты 4 порядка,
• параллельная OpenMP-версия с реализацией решения задачи (1-3) методом Гаусса – Лежандра.
Входные параметры задаются через специальный входной файл, имя которого может быть произвольным и указывается при запуске задачи. В этом файле в произвольной последовательности задаются:
• Нормализованная частота магнитного резонанса (OmegaF),
• Минимальное значение параметра диссипации (alpha_min) (только для G, α,
• Максимальное значение параметра диссипации (alpha_max) (только для G, α),
• Шаг параметра диссипации (alpha_step) (только для G, α),
• Минимальное значение параметра спин-орбитальной связи (r_min) (только для G, r),
• Максимальное значение параметра спин-орбитальной связи (r_max) (только для G, r),
• Шаг параметра спин-орбитальной связи (r_step) (только для G, r),
• Минимальное отношение джозефсоновской энергии к энергии магнитной анизотропии (G_min),
• Максимальное отношение джозефсоновской энергии к энергии магнитной анизотропии (G_max),
• Шаг отношения джозефсоновской энергии к энергии магнитной анизотропии (G_step).
Остальные параметры могут быть изменены при необходимости непосредственно в исходном коде программы.
Результаты выполнения программы записываются, в зависимости от выбора расчетной плоскости, в файлы
points_GA_mz_m1.dat или points_Gr_mz_m1.dat и содержат координаты точек на плоскости параметров соответственно (G, α) или (G, r), в которых происходит переворот магнитного момента.
Файлы points_GA_mz_p1.dat или points_Gr_mz_p1.dat содержат точки, в которых переворот не зафиксирован. В первой колонке файлов обоих версий содержатся значения отношения джозефсоновской энергии к энергии магнитной анизотропии G, во второй колонке содержатся значения параметра диссипации alpha (только для случая расчета на плоскости (G, α)) или значения параметра спин-орбитальной связи r (только для расчета на плоскости (G, r)). В третьей колонке содержатся абсолютные значения магнитного момента.
Архив включает, программы на MPI-С++ и OpenMP-C++, скрипт для компиляции и запуска программы, результат работы программы в виде выходных файлов с данными, полученными для заданных в качестве примера входных параметров, а также файл readme с подробным описанием порядка запуска и пояснением к примеру.
Архив программы
Литература:
- Атанасова П.Х., Панайотова С.А., Рахмонов И.Р., Шукринов Ю.М., Земляная Е.В., Башашин М.В. Периодичность в возникновении интервалов переворота магнитного момента φ0 перехода // Письма в ЖэТФ, Т.110, №11, 736-740, 2019.
- Башашин М.В., Земляная Е.В. Сравнительный анализ производительности MPI- и OpenMP-программ на примере параллельных расчетов в рамках модели ядро-ядерного потенциала и модели φ0-спинтроники // Современные информационные технологии и ИТ-образование. Т.18, №3, 545-557, 2022.




