
|
Language: Fortran
TIME6T 1.0 - numerical solutions 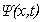 of the Cauchy problem for the
time-dependent Schroedinger equation in the finite spatial variable
interval of the Cauchy problem for the
time-dependent Schroedinger equation in the finite spatial variable
interval 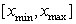
TIME6T 2.0 - numerical solutions 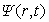 of the Cauchy problem for the
multidimensional time-dependent Schroedinger equation. of the Cauchy problem for the
multidimensional time-dependent Schroedinger equation.
TIME6T 1.0 - numerical solutions 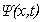 of the Cauchy problem of the Cauchy problem
for the time-dependent Schroedinger equation
The subroutine TIME6T 1.0 calculates numerical solutions 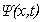 of the Cauchy
problem for the time-dependent Schroedinger equation in the finite spatial
variable interval of the Cauchy
problem for the time-dependent Schroedinger equation in the finite spatial
variable interval 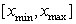
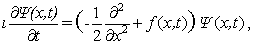
with the initial condition 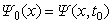 up to 2M (M=1, 2, 3) order of accuracy in the time step
up to 2M (M=1, 2, 3) order of accuracy in the time step 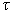 of a uniform
grid of a uniform
grid 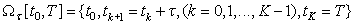 , covering the time
interval , covering the time
interval 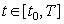 , using the explicit Magnus expansion [1] of the
evolution operator with the additional gauge transformations and their
Pade approximations. , using the explicit Magnus expansion [1] of the
evolution operator with the additional gauge transformations and their
Pade approximations.
The considered scheme was constructed on the basis of the algorithms
published in paper [2]. Further discretization of the resulting problem
is implemented by means of the finite-element method [3], using Lagrange
interpolation polynomials up to the order p=8 at suitable smoothness
of the solution.
References:
- Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
- Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
- Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
Structure:
| Type |
- |
SUBROUTINE |
| Name |
- |
TIME6T |
| Internal subroutines |
- |
TMSOLV, ASSMBS, ASSMBM, EMASSD, ESTIFD, ADDVEC, BOUNDC, COLMHT, ERRDIM, FEGRID, MAXHT, GAULEG, NODGEN, SHAPEF, MULTC, MULTCC, REDBAC, DECOMC |
| External subroutines |
- |
POTCAL, DINIT (user-supplied subroutines) |
Usage:
CALL TIME6T (TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,FMATR,IOUM,
EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,RMESH,IOUT,FMATR,IOUM,
EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT
where:
| TITLE |
- |
character symbol, title of the run to be printed on the output listing. |
| NPOL |
- |
integer number, order of interpolating Lagrange polynomials. |
| TMIN |
- |
double precision number, begin of time interval. |
| TMAX |
- |
double precision number, end of time interval. |
| TAU |
- |
double precision number, time step of time variable t. |
| ITORDR |
- |
integer number, order of Magnus expansion, 1 , 2 , 3. |
| IPRINT |
- |
integer number, level of print, 0 , 1 , 2. |
| IPRSTP |
- |
integer number, step of spatial variable x with which solutions are printed out. |
| IPRITT |
- |
integer number, step of time variable t with which solutions are printed out. |
| NMESH |
- |
integer number, dimension of array RMESH. NMESH always should be odd and > = 3. |
| RMESH |
- |
double precision array, array RMESH contains information about
subdivision of interval [x_min,x_max] of space variable x on
subintervals. The whole interval [x_min,x_max] is divided as
follows: RMESH(1) = x_min, RMESH(NMESH) = x_max, and the values
of RMESH(I) set the number of elements for each subinterval
[RMESH(I-1), RMESH(I+1)], where I=2, 4, ... , NMESH-1. |
| IBOUND |
- |
integer number, parameter defining the type of boundary
conditions set in the boundary points x = x_min and x = x_max:
= 1 - the Dirichlet - Dirichlet boundary conditions;
= 2 - the Dirichlet - Neumann boundary conditions;
= 3 - the Neumann - Dirichlet boundary conditions;
= 4 - the Neumann - Neumann boundary conditions. |
| FNOUT |
- |
character symbol, name of the output file for printing out the results of the calculation. |
| IOUT |
- |
integer number, number of the output logical device for printing out the results of the calculation. |
| FMATR |
- |
character symbol, name of the scratch file for storing matrices. |
| IOUM |
- |
integer number, number of the logical device for storing matrices. |
| EVWFN |
- |
character symbol, name of the output file for storing the results
of the calculation, namely, finite-element grid points, and
solutions. It is used only if IOUF > 0. |
| IOUF |
- |
integer number, number of the logical device for storing data into file EVWFN. |
| TOT |
- |
double precision array, working vector. |
| ITOT |
- |
integer array, working vector. |
| ZTOT |
- |
double complex array, working vector. |
| MTOT |
- |
integer number, dimension of the working array TOT. |
| MITOT |
- |
integer number, dimension of the working array ITOT. |
| MZTOT |
- |
integer number, dimension of the working array ZTOT. |
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
| NGRID |
- |
integer number, the number of finite-element grid points. |
| NN |
- |
integer number, the number of finite-element grid points of solution. |
| TT |
- |
double precision number, the value of time variable t. |
| TAU |
- |
double precision number, the time step of time variable t. |
| XGRID |
- |
double precision array, contains the values of the finite-element grid points. |
| ZU |
- |
double complex array, contains calculated solution. |
Example 1: subroutine POTCAL for the given potential
f(x,t) = (4 - 3 * exp(-t)) * x**2 / 2 .
SUBROUTINE POTCAL(RG,TT,TAU,DA,HH,DS,SS,ITORDR)
IMPLICIT REAL*8 (A-H,O-Z)
DATA ZERO / 0.D0 /, ONE / 1.D0 /
HH = (4 - 3 * DEXP(-TT)) * RG**2 / 2
SS = ZERO
DA = ONE / 2
DS = ZERO
IF (ITORDR .GE. 2) THEN
F1 = -3 * DEXP(-TT) / 24 * RG**2 / 2
HH = HH + TAU**2 * F1
F1 = 3 * DEXP(-TT) / 12 * RG**2 / 2
SS = SS + TAU**2 * F1
END IF
IF (ITORDR .GE. 3) THEN
F1 = -3 * DEXP(-TT) * RG**2 / 2 / 1920
1 + ( 3 * DEXP(-TT) * RG)**2 / 1440
2 - (-3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
HH = HH + TAU**4 * F1
F1 = 3 * DEXP(-TT) * RG**2 / 2 / 480
1 + (3 * DEXP(-TT) * RG) * (4 - 3 * DEXP(-TT)) * RG / 720
SS = SS + TAU**4 * F1
DA = DA + (- 3 * DEXP(-TT)) * TAU**4 / 720
DS = DS - ( 3 * DEXP(-TT)) * TAU**4 / 720
END IF
RETURN
END
| RG |
- |
double precision number, the value of spatial variable x. |
| TT |
- |
double precision number, the value of time variable t. |
| TAU |
- |
double precision number, the time step of time variable t. |
| HH |
- |
double precision number, contains the operator A^(M)_k without
differential operators at M=ITORDR. |
| SS |
- |
double precision number, contains the operator S^(M)_k without
differential operators at M=ITORDR. |
| DA |
- |
double precision number, contains the coefficient of differential
operators of operator A^(M)_k at M=ITORDR.
DA = 1/2 at ITORDR = 1, 2,
while DA = 1/2 + f_{xxtt}(x,t) * TAU**4 / 720 at ITORDR = 3. |
| DS |
- |
double precision number, contains the coefficient of differential
operators of operator S^(M)_k at M=ITORDR.
DS = 0 at ITORDR = 1 , 2,
while DS = - f_{xxt}(x,t) * TAU**4 / 720 at ITORDR = 3. |
Here parameters RG, TT, TAU should not be changed by users.
Example 2: subroutine DINIT for given initial condition
psi_0(x) = sqrt(sqrt(1 / pi)) * exp( - (x - sqrt(2))**2 / 2) .
SUBROUTINE DINIT(KEY,NN,NGRID,XGRID,ZU1)
IMPLICIT REAL*8 (A-H,O-Y)
IMPLICIT COMPLEX*16 (Z)
DIMENSION ZU1(NN),XGRID(NGRID)
DATA ONE / 1.D0 /, TWO / 2.D0 /
PI = DACOS(- ONE)
FG = DSQRT(DSQRT(ONE / PI))
DO I = 1 , NN
X = XGRID(I + KEY)
ZU1(I) = FG * DEXP( - (X - DSQRT(TWO))**2 / 2)
END DO
RETURN
END
KEY - integer number, If IBOUND >= 3 then KEY = 0, else KEY = 1.
Here parameters KEY, NN, NGRID, XGRID should not be changed by users.
Remarks:
- In subroutine TIME6T 1.0 is used the dynamic distribution storages as
one-dimensional arrays TOT, ZTOT ITOT, RMESH. In test example their
dimension is set by the values MTOT=100000, MZTOT=100000, MITOT=100000,
NMESH1=5. If user has set insufficient values of dimension above arrays
the message about an error is printed and the execution of the program
is aborted. In the last case, in order to carry out the required
calculation it is necessary to increase the dimensions of arrays to the
quantity taken from the message.
- For the accuracy control over the numerical solution by step TAU,
the Runge coefficient on four twice condensed grids is additionally
calculated, using the subroutine RUNGE.
Sources TIME6T 1.0 with example and detailed description (pdf) are submitted.
TIME6T 2.0 - numerical solutions 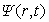 of the Cauchy problem of the Cauchy problem
for the multidimensional time-dependent Schroedinger equation
The subroutine TIME6T 2.0 calculates numerical solutions 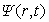 of the Cauchy
problem for the time-dependent Schroedinger equation in d-dimensional space of the Cauchy
problem for the time-dependent Schroedinger equation in d-dimensional space
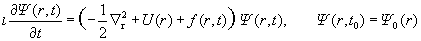
up to 2M (M=1, 2, 3) order of accuracy in the time step 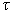 of a uniform grid
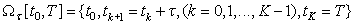
covering the time interval
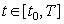 , in the frame of the Kantorovich method [1] using the explicit
Magnus expansion [2] of the evolution operator with the additional gauge
transformations and their Pade approximations.
The considered scheme was constructed on the basis of the algorithms
published in [3]. Further discretization of the resulting problem is
implemented by means of the finite-element method [4] using Lagrange
interpolation polynomials up to the order p=8 at suitable smoothness
of the solution. Test example is carried out from paper [5].
References:
- Kantorovich L.V. and Krylov V.I. Approximate Methods of Higher Analysis.
New York, Wiley, 1964.
- Magnus W. Commun. Pure Appl. Math., 1954, v. 7, pp. 649-673.
- Chuluunbaatar O. et al. J. Phys. A, 2008, v. 41, pp. 295203-1-25.
- Bathe K.J. Finite element procedures in engineering analysis.
Englewood Cliffs, Prentice Hall, New York, 1982.
- Chuluunbaatar O. et al. Phys. Rev E, 2008, v. 78, pp. 017702-1-4.
Structure:
| Type |
- |
SUBROUTINE |
| Name |
- |
TIME6T |
| Internal subroutines |
- |
TMSOLV, ASSMBN, ASSMBT, EMASSD, ESTIFD, ESTIFN,
ESTITD, ESTITN, ADDVEC, HQPOTN, SGPOTN, BOUNDC,
COLMHT, ERRDIM, FEGRID, MAXHT, GAULEG, NODGEN,
SHAPEF, MULTC, MULTCC, REDBAC, DECOMC |
| External subroutines |
- |
POTCAL, POTTIM, DINIT (user-supplied subroutines) |
Usage:
CALL TIME6T (TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,
POTEN,IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT)
INPUT: TITLE,MDIM,IDIM,NPOL,TMIN,TMAX,TAU,ITORDR,IPRINT,IPRSTP,IPRITT,NMESH,RMESH,IBOUND,FNOUT,IOUT,POTEN,
IOUP,POTTM,IOUD,FMATR,IOUM,EVWFN,IOUF,TOT,ITOT,ZTOT,MTOT,MITOT,MZTOT
where:
| TITLE |
- |
character symbol, title of the run to be printed on the output listing. |
| MDIM |
- |
integer number, number of coupled differential equations. |
| IDIM |
- |
integer number, dimension of the envelope space. |
| NPOL |
- |
integer number, order of interpolating Lagrange polynomials. |
| TMIN |
- |
double precision number, begin of time interval. |
| TMAX |
- |
double precision number, end of time interval. |
| TAU |
- |
double precision number, time step of time variable t. |
| ITORDR |
- |
integer number, order of Magnus expansion, 1 , 2 , 3. |
| IPRINT |
- |
integer number, level of print, 0 , 1 , 2. |
| IPRSTP |
- |
integer number, step of spatial variable r with which solutions
are printed out. |
| IPRITT |
- |
integer number, step of time variable t with which solutions
are printed out. |
| NMESH |
- |
integer number, dimension of array RMESH. NMESH always should be
odd and > = 3. |
| RMESH |
- |
double precision array, array RMESH contains information about
subdivision of interval [0,r_max] of space variable x on
subintervals. The whole interval [0,r_max] is divided as
follows: RMESH(1) = 0, RMESH(NMESH) = r_max, and the values
of RMESH(I) set the number of elements for each subinterval
[RMESH(I-1), RMESH(I+1)], where I=2, 4, ... , NMESH-1. |
| IBOUND |
- |
IBOUND - integer number, parameter defining the type of boundary
conditions set in the boundary points r = 0 and r = r_max:
= 1 - the Dirichlet - Dirichlet boundary conditions;
= 2 - the Dirichlet - Neumann boundary conditions;
= 3 - the Neumann - Dirichlet boundary conditions;
= 4 - the Neumann - Neumann boundary conditions. |
| FNOUT |
- |
character symbol, name of the output file for printing out
the results of the calculation. |
| IOUT |
- |
integer number, number of the output logical device for printing
out the results of the calculation. |
| POTEN |
- |
character symbol, name of the scratch file for potential matrices. |
| IOUP |
- |
integer number, number of the logical device POTEN. |
| POTTM |
- |
character symbol, name of the scratch file for potential matrices. |
| IOUD |
- |
integer number, number of the logical device POTTM. |
| FMATR |
- |
character symbol, name of the scratch file for storing matrices. |
| IOUM |
- |
integer number, number of the logical device FMATR. |
| EVWFN |
- |
character symbol, name of the output file for storing the results
of the calculation, namely, finite-element grid points, and
solutions. It is used only if IOUF > 0. |
| IOUF |
- |
integer number, number of the logical device EVWFN. |
| TOT |
- |
double precision array, working vector. |
| ITOT |
- |
integer array, working vector. |
| ZTOT |
- |
double complex array, working vector. |
| MTOT |
- |
integer number, dimension of the working array TOT. |
| MITOT |
- |
integer number, dimension of the working array ITOT. |
| MZTOT |
- |
integer number, dimension of the working array ZTOT. |
OUTPUT: WRITE(IOUF) NN,NGRID,TT,TAU,(XGRID(J),J=1,NGRID),(ZU(J),J=1,NN)
| NGRID |
- |
integer number, the number of finite-element grid points. |
| NN |
- |
integer number, the number of finite-element grid points of solution. |
| TT |
- |
double precision number, the value of time variable t. |
| TAU |
- |
double precision number, the time step of time variable t. |
| XGRID |
- |
double precision array, contains the values of the finite-element grid points. |
| ZU |
- |
double complex array, contains calculated solution. |
POTCAL is the name of the user-supplied subroutine which calculates
the potential matrices V and Q.
POTTIM is the name of the user-supplied subroutine which calculates
the potential matrices G and Z.
DINIT is the name of the user-supplied subroutine which calculates
the initial function.
Remarks:
- In subroutine TIME6T 2.0 is used the dynamic distribution storages as
one-dimensional arrays TOT, ZTOT, ITOT, RMESH. In test example their
dimension is set by the values MTOT=2 000 000, MZTOT=1 000 000,
MITOT=300 000, NMESH1=5. If user has set insufficient values of dimension
above arrays the message about an error is printed and the execution of
the program is aborted. In the last case, in order to carry out the
required calculation it is necessary to increase the dimensions of arrays
to the quantity taken from the message.
- For the accuracy control over the numerical solution by step TAU, the Runge
coefficient on four twice condensed grids is additionally calculated, using
the subroutine RUNGE.
Sources TIME6T 2.0 with example and detailed description (pdf) are submitted.


|

|

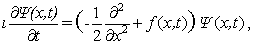
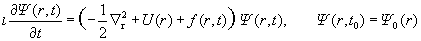
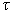 of a uniform grid
of a uniform grid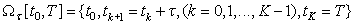
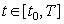 , in the frame of the Kantorovich method [1] using the explicit
Magnus expansion [2] of the evolution operator with the additional gauge
transformations and their Pade approximations.
, in the frame of the Kantorovich method [1] using the explicit
Magnus expansion [2] of the evolution operator with the additional gauge
transformations and their Pade approximations.




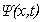 of the Cauchy problem for the
time-dependent Schroedinger equation in the finite spatial variable
interval
of the Cauchy problem for the
time-dependent Schroedinger equation in the finite spatial variable
interval 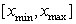
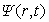 of the Cauchy problem for the
multidimensional time-dependent Schroedinger equation.
of the Cauchy problem for the
multidimensional time-dependent Schroedinger equation.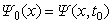 up to 2M (M=1, 2, 3) order of accuracy in the time step
up to 2M (M=1, 2, 3) order of accuracy in the time step