Язык: Фортран
Подпрограмма ZHYPG2 вычисляет гипергеометрические функции 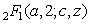 с комплексными параметрами
с комплексными параметрами 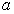 ,
, 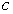 и комплексным аргументом
и комплексным аргументом 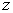 [1]. Для
вычисления гипергеометрической функции
[1]. Для
вычисления гипергеометрической функции 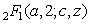 используются заранее
вычисленные с помощью подпрограммы HYPGEO [2] значения гипергеометрических
функций и их производных в точках:
используются заранее
вычисленные с помощью подпрограммы HYPGEO [2] значения гипергеометрических
функций и их производных в точках:
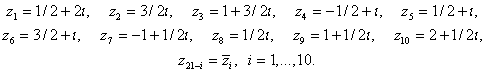
Алгоритм, на основе которого была построена данная процедура, опубликован
в работе [3]. Предлагаемый алгоритм позволяет сэкономить время вычисления
многократных интегралов, подинтегральная функция которых содержит
гипергеометрические функции 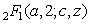 , примерно в 10-60 раз в
зависимости от точности вычисления (10-4-10-14) по сравнению с прямым
использованием подпрограммы HYPGEO при каждом значении
, примерно в 10-60 раз в
зависимости от точности вычисления (10-4-10-14) по сравнению с прямым
использованием подпрограммы HYPGEO при каждом значении 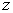 . Подобные
вычисления встречаются при исследовании однократной и двукратной ионизации
электронным ударом двухатомных молекул (см. работы [4,5]).
. Подобные
вычисления встречаются при исследовании однократной и двукратной ионизации
электронным ударом двухатомных молекул (см. работы [4,5]).
Литература:
- Абрамовиц М. и Стиган И. Справочник по специальным функциям. Москва,
Наука, 1979, стр.370.
- Press W.H., Teukolsky S.A., Vetterling W.T. and Flannery B.P.
Numerical recipes: The art of scientific computing.
Cambridge University Press, Cambridge, 1986.
- Чулуунбаатар О. Вестник ТвГУ: Серия Прикладная Математика. 2008,
№ = 26(86), стр. 47-64.
- Chuluunbaatar O., Joulakian B.B., Tsookhuu Kh. and Vinitsky S.I.
J. Phys. B, 2004, v. 37, pp. 2607-2616.
- Chuluunbaatar O., Joulakian B.B., Puzynin I.V., Tsookhuu Kh. and
Vinitsky S.I. J. Phys. B, 2008, v. 41, pp. 015204-1-6.
Структура:
| Тип |
- |
FUNCTION |
| Имена входа для пользователя |
- |
ZHYPG2 |
| Внутренние подпрограммы |
- |
ZSUM, ZGAMMA, DRHYP, CGAMA, HYPGEO, HYPDRV, HYPSER, ODEINT, BSSTEP, MMID, PZEXTR |
Обращение:
ZFUNC = ZHYPG2(ZA,ZC,ZZ,NMAX,EPS)
INPUT: ZA, ZC, ZZ, NMAX, EPS, где:
| ZA |
- |
комплексная переменная, содержит значение параметра 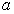 . . |
| ZC |
- |
комплексная переменная, содержит значение параметра 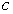 . . |
| ZZ |
- |
комплексная переменная, содержит значение аргумента 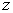 . . |
| NMAX |
- |
целочисленная переменная, максимальное число суммирования усеченного ряда Гаусса. |
| EPS |
- |
вещественная переменная, точность вычислений. |
Архив программы с описанием (.pdf) и исходными текстами.
В архиве содержится пример вычисления интергала:
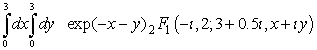




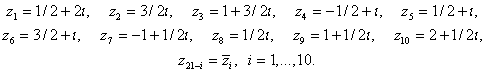
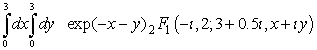





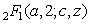 с комплексными параметрами
с комплексными параметрами 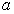 ,
, 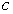 и комплексным аргументом
и комплексным аргументом 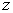 [1]. Для
вычисления гипергеометрической функции
[1]. Для
вычисления гипергеометрической функции