Language: C++
Environment: Microsoft Visual Studio

---

The program is designed to calculate closed equilibrium orbits in an isochronous cyclotron by solving of the equations of motion. The equations of motion are the system of three nonlinear differential equations of the second order with differentiation by time [1]. The equations of motion are solved by the Runge-Kutta method. Initial conditions are calculated using analytical formulas [1]. The selection of integration step is carried out manually (h/2). The numerical solution of the equations of motion in dimensionless representation allows us to calculate the rotation frequency of equilibrium particle in closed equilibrium orbits depending on her kinetic energy and to evaluate the quality of forming of magnetic field of an isochronous cyclotron.

The program is written in C ++ in the MS Visual Studio 2019 environment in the SDI standard and uses the technology of parallel computations. The program contains predefined initial data for two operating multi-purpose isochronous cyclotrons AIC-144 (INP PAS, Poland) and AVF (Riken, Japan). Both accelerators have well-formed magnetic fields with insignificant value of the first harmonic. In the example in program archive, we used the test map of the magnetic field formed for the main operating mode of AIC-144: p; Ek~60,7 MeV. When forming of the test map of the magnetic field for the certain level of current in the main coil, 63 magnetic field maps measured for 3 levels of current in the main coil and the second-degree Lagrange interpolation polynomial were used. When calculating of the particle rotation frequency, the interpolation of the formed test map of the magnetic field was carried out using the method of cubic splines (in radius and azimuth).

The program interface is presented in Fig. 1. As initial data, the program enters the path of the formed/measured magnetic field map, the name of accelerated particle, the initial and final kinetic energies, the kinetic energy step, the frequency of RF generator, the harmonic number, the number of magnetic sectors, the sign of charge, the number of elementary charges, the particle mass in standard atomic mass units and the integration step. Since the equations of motion with differentiation by time are reduced to the dimensionless form, the initial and final times of isochronous particle are presented in radians. The results of calculations in the form of graph and text file are presented in Fig. 2,3. The calculation results can also be written in the binary format. In the text file, Ek is the kinetic energy of particle. Rev is the equivalent radius of closed equilibrium orbit. Rmn is the mean radius of closed equilibrium orbit. F0 is the particle rotation frequency in closed equilibrium orbits. dReo is the closure accuracy of closed equilibrium orbit. A relative error is considered as relation of difference between obtained and isochronous values to isochronous value. The relative errors of the mean magnetic field and t he particle rotation frequency depending on the mean radius of closed equilibrium orbit are presented in Fig. 4. The mean magnetic field is calculated along circle defined by the mean radius of closed equilibrium orbit.

Fig. 1. EORP 2020 program interface.

Fig. 2. The particle rotation frequency depending on the mean radius of closed equilibrium orbit.

Fig. 3. The calculation results.

Fig. 4. The relative errors of the mean magnetic field and the rotation frequency of charged particle
depending on the mean radius of closed equilibrium orbit.

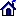
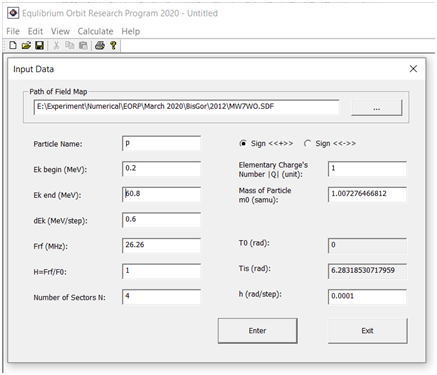
A correctly formed magnetic field ensures successful acceleration of particles without manual adjustment of currents in trim coils of a multi-purpose isochronous cyclotron. With the integration step h = 1E-4, the accuracy of calculating of particle rotation frequency is not worse than 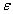= 2E-6. With the measurement accuracy of one magnetic field map 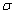= 1í4, the value of modulus of difference in the values of SigmaBmn and SigmaF0 curves in the range from the ion source to the electrostatic deflector of AIC-144 (from ~3 to 62,8 cm) is within |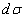|<3í4, that says about the correctness of the magnetic field formation.

Download program and initial data.

References:

1. I.V. Amirkhanov, G.A. Karamysheva, I.N. Kiyan, and J. Sulikowski. Calculation of Proton Rotation Frequency in Static Equilibrium Orbits at the Isochronous Cyclotron. // Physics of Particles and Nuclei Letters, 2015, Vol. 12, No.3, pp. 428431. (English translation).

---