 |
The Fitter is designed to be used for SANS data processing first of all. Thus, SANS theoretical models are implemented in it. Moreover, some standard mathematical models are added for wider applicability. Besides the implemented theoretical models, Fitter has a minimization module. It provides a safe call of MINUIT [25] procedures in the current version. The important feature of Fitter's design is its expandability: both new models and new minimizing algorithms can easily be added to the existing ones.
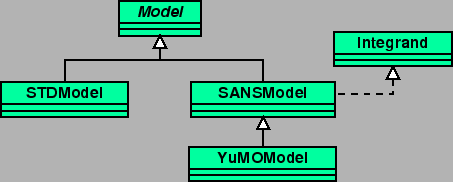
Fitter's model module is designed as follows (fig.1).
Abstract base class Model provides a common interface,
used by a minimization module.
Thus, any theoretical model class inherits from it.
Model classes currently implemented in the Fitter are:
STDModel, SANSModel, YuMOModel.
Each concrete class provides several theoretical functions.
All of them are described below.
Standard mathematical models implemented in the Fitter are:
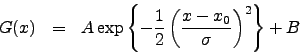
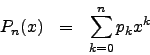
Determination of invariants for small-angle scattering curves allows one to analyze the structure of a particle under study. Upon the first step of this analysis the particle form is approximated by simple geometrical bodies - ellipsoids, cylinders, prisms.
Thus, SANS models implemented in the Fitter are:
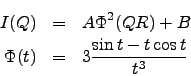
![\begin{eqnarray*}
I(Q) &=&
A \int\limits_{0}^{1} \Phi^2\left[ Qa\sqrt{1+x^2(v^2-1)} \right] dx + B \\
\Phi(t) &=& 3\frac{\sin t-t\cos t}{t^3}
\end{eqnarray*}](img10.gif)
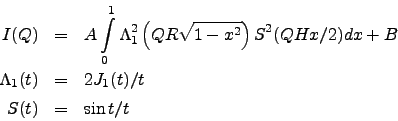
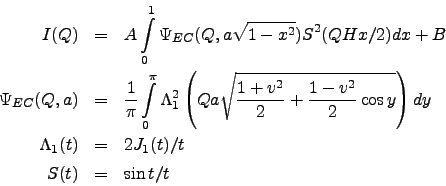
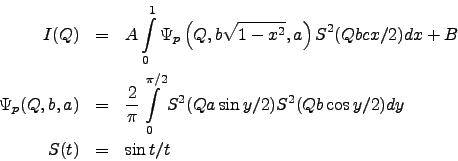
![\begin{eqnarray*}
I(Q) &=&
A \left[ \Phi(QR_1)-\left(\frac{R_2}{R_1}\right)^3\Phi(QR_2) \right]^2 + B \\
\Phi(t) &=& 3\frac{\sin t-t\cos t}{t^3}
\end{eqnarray*}](img19.gif)
More detailed information about SANS models is available in [22].
These models are implemented to fit data measured on the YuMO spectrometer [23] operated on the 4-th channel of the fast pulsed reactor IBR-2 [24]. YuMO models are the same as SANS, but they take into account the spectrometer resolution.
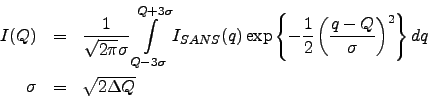
To find theoretical model parameters, one should minimize a functional, which is a measure of deviation between a theoretical curve and experimental data. In a common case of a least-squares fit, the functional under minimization is a chi-square:
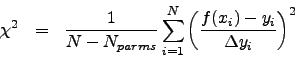
We are using ROOT::TMinuit class to perform a minimization. This package was originally written in Fortran by Fred James and part of PACKLIB (patch D506) and has been converted to a C++ class by R.Brun. The current implementation in C++ is a straightforward conversion of the original Fortran version. The main changes are:
Additional modifications were made to separate TMinuit class from the ROOT package (Fitter is ROOT independent indeed).
MINUIT offers the user a choice of several minimization algorithms. The MIGRAD algorithm is, in general, the best minimizer for nearly all functions. It is a variable-metric method with inexact line search, a stable metric updating scheme, and checks for positive-definiteness. Its main weakness is that it depends heavily on knowledge of the first derivatives, and fails miserably if they are very inaccurate.
For further details see MINUIT documentation [25].
The least-squares fitting involves the minimization of the sum of the squared residuals. There are two instances where this minimization produces less than satisfactory fit:
Robust estimates designed to be successful in such cases. The essence of robust fitting is to use a minimization that is less influenced by outliers and the dynamic range of the Y-variable. Each data measured point took into account with it own weight, which indicate influence of given point.
It is based on so-called M-estimates which follow from maximum like-hood
approach, M-estimates are usually the most relevant for model fitting.
Robust approach uses gross-error model (Hubert).
Probability distribution function of measurement errors ![]() suggested
as a superposition of two distributions: basic
suggested
as a superposition of two distributions: basic ![]() and distribution
of big errors
and distribution
of big errors ![]()
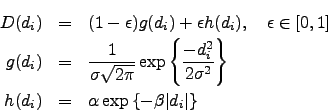
In practice, robustness works also in cases of other distributions ![]() ,
for example, normal one like
,
for example, normal one like ![]() is, but with bigger RMS.
is, but with bigger RMS.
Application of maximum like-hood approach and few simplifications and the
fact that RMS of the distribution ![]() can be approximated by
chi-square of data points, give us well known Tukey bi-square weights,
which is suitable in most cases.
can be approximated by
chi-square of data points, give us well known Tukey bi-square weights,
which is suitable in most cases.
In chi-square function data values are multiplied by their weights:
The initial values of the weights are equal to 1. In the following iterations, weights are recalculated after each procedure of minimization and calculation of the new value of chi-square. Iterations are repeated until convergence (until chi-square value is stabilized within a predefined accuracy).
In general, the robust approach looks like:
For detailed explanation see [26,27,28].