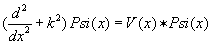|
Язык: Фортран
Подпрограмма SCATTERH6 вычисляет фазовый сдвиг delta
и волновые функции Psi уравнения Шредингера
с граничными условиями:
Psi(x) -> 0 при x -> 0 или x -> - бесконечности,
Psi(x) -> sin (kx + delta) при x -> + бесконечности
на равномерной сетке узлов по квадратурной формуле Боде [1] заданного
(от 2 до 6) порядка точности по шагу h на равномерной сетке.
Структура:
| Тип |
- |
SUBROUTINE |
| Имена входа для пользователя |
- |
SCATTERH6 |
| Внутренние имена |
- |
RSTEP, XIVALUE1, PHI0, PHI1, GAUSSJ, MUU |
| Используемые внешние программы |
- |
POT, INITIAL - подпрограммы пользователя |
Обращение:
CALL SCATTERH6(DLAM1,PSI0,QQ,RMIN,RMAX,R,NN,IPOINT,EPS)
Входные данные - QQ,RMIN,RMAX,R,NN,IPOINTS,EPS, где:
| QQ |
- |
заданный импульс; |
| RMIN, RMAX |
- |
минимальное и максимальное значения независимой
переменной R на конечном интервале [RMIN, RMAX]; |
| R(I) |
- |
узлы сетки; |
| NN |
- |
число подинтервалов; |
| IPOINT |
- |
количество узлов квадратурной формулы Боде (от 2 до 6); |
| EPS |
- |
точность выполнения итерационного процесса. |
Выходные данные - DLAM1, PSI0, где:
| DLAM1 |
- |
значения фазового сдвига delta; |
| PSI0(I) |
- |
значения волновой функции Psi(R(I)). |
| FUNCTION POT(R) |
- |
составляется пользователем для вычисления
потенциальной функции V(x). |
SUBROUTINE INITIAL
(PSI0,DLAM0,QQ,R,IPOINT,N) |
- |
составляется пользователем для вычисления асимптотики волновых
функций PSI0(1)...PSI0(IPOINT-1), начальных
приближений волновых функций PSI0(IPOINT)...PSI0(N)
и фазового сдвига DLAM0. |
Метод:
Алгоритм, на основе которого была построена данная подпрограмма,
опубликован в работах [2-4].
Точность вычислений - до O(h^(2[(IPOINT+1)/2]).
Архив программы с исходными текстами.
Литература:
- М. Абрамовиц, И. Стиган, Справочник по специальным функциям.
М.: Наука, 1979, стр. 682-683.
- O. Chuluunbaatar, I.V. Puzynin, S.I. Vinitsky, Journal of
Computational Methods in Sciences and Engineering, 2002, v.2, p.37.
- О.Чулуунбаатар, И.В. Пузынин, С.И. Виницкий, Препринт ОИЯИ,
P11-2001-61, Дубна, 2001.
- О.Чулуунбаатар, Автореферат, 11-2002-209, Дубна, 2002.



|

|