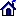Language: Fortran

---

The subroutine SCATTERH6 calculating a phase shift delta and wave functions Psi of the Schroedinger equations

with boundary conditions:

on a uniform grid by the Bode quadrature formula [1] with a given order of accuracy (from 2 up to 6) by the step h on a uniform grid.

Structure:

Type	-	SUBROUTINE
User Entry Names	-	SCATTERH6
Internal Names	-	RSTEP, XIVALUE1, PHI0, PHI1, GAUSSJ, MUU
External References	-	POT, INITIAL - user-supplied subprograms

Usage:

CALL SCATTERH6(DLAM1,PSI0,QQ,RMIN,RMAX,R,NN,IPOINT,EPS)

The input datas - QQ, RMIN, RMAX, R, NN, IPOINTS, EPS, where:

QQ	-	is given momentum;
RMIN, RMAX	-	are minimal and maximal values of independent variable R on a finite interval [RMIN, RMAX];
R(I)	-	are nodes of a grid;
NN	-	is number of subintervals;
IPOINT	-	is number of nodes of the Bode quadrature formula (from 2 up to 6);
EPS	-	is given accuracy of a calculation process.

Output datas - DLAM1, PSI0, where:

DLAM1	-	is value of a phase shift delta;
PSI0(I)	-	are values of a wave function Psi(R(I)).

FUNCTION POT(R)	-	is compounded by the user for calculation of the potential function V(x).
SUBROUTINE INITIAL (PSI0,DLAM0,QQ,R,IPOINT,N)	-	is compounded by the user for calculation of asymptotic wave functions PSI0(1)...PSI0(IPOINT-1), initial approximations: of wave functions PSI0 (IPOINT)... PSI0 (N) and a phase shift DLAM0.

Method:

Algorithm, on the basis of which the given subroutine was constructed described in [2-4].
The accuracy of calculation - up to O (h ^ (2 [(IPOINT+1) /2]).

Sources are submitted.

References:

1. M. Abramowitz, I. Stegun, Handbook of mathematical functions, National Bureau of Standarts, NY, 1964.
2. O. Chuluunbaatar, I.V. Puzynin, S.I. Vinitsky, Journal of Computational Methods in Sciences and Engineering, 2002, v.2, p.37.
3. O. Chuluunbaatar, I.V. Puzynin, S.I. Vinitsky, JINR preprint P11-01-61, Dubna 2001.
4. O. Chuluunbaatar, JINR abstract 11-2002-209, Dubna, 2002.

---