Введение

Успешно работающий модернизированный спектрометр ЮМО (4-й канал ИБР-2) [1] оснащен новой программой первичной обработки данных. Несмотря на то, что базовые процедуры (Останевич Ю.М., Беззаботнов В.Ю., 1992 год, неопубликованное, кратко на сайте [2]) оставлены практически без изменения, новая программа содержит, помимо современных дизайна и реализации, ряд особенностей. Существенное расширение числа пользователей установки ЮМО диктует необходимость не только в документации для ее программного обеспечения, но и в решении некоторых задач, тесно связанных с обработкой экспериментальных данных. Модернизация инструмента еще не завершена, и поэтому ряд вопросов будет оставлен за рамками обсуждения. Это касается прежде всего форматов исходных данных и объединения данных с двух детекторов, на установке, работающей в двухдетекторном варианте [3]. Для обработки экспериментальных данных, полученных на спектрометре ЮМО, можно также воспользоваться программой OpenG2 [4], написанной на основе пакета PV-WAVE [5], с упрощенным алгоритмом обработки. Новая программа SAS скоррелирована с программным обеспечением спектрометра ЮМО [6,7] и будет развиваться в соответствии с модернизацией установки.

Общий формализм и малоугловое рассеяние нейтронов

Прежде чем изложить математическую сторону формализма малоуглового рассеяния нейтронов, обсудим некоторые ключевые положения первичной обработки экспериментальных данных. Исходные файлы, полученные на спектрометре, содержат зависимости номер канала -- счет для всех колец детекторов рассеяния (см. схему ниже). Программа первичной обработки должна перевести номер канала сначала в длину волны, а затем -- в переданный импульс нейтрона, а счета на детекторах -- в сечение когерентного рассеяния. Первая часть задачи решается путем простого пересчета номера канала сначала во время пролета, а затем, при известных расстояниях замедлитель -- детектор, образец -- детектор и радиус соответствующего кольца, -- в переданный импульс. Решение второй задачи требует проведения, помимо измерения рассеяния нейтронов от изучаемого образца, дополнительного эксперимента со стандартным рассеивателем. Для этого на большинстве малоугловых инструментов помещают в позицию образца, например, воду. Особенностью спектрометра ЮМО является не только геометрия установки (аксиально-симметричная) и наличие отверстий в центральной части детекторов для прохождения прямого пучка, но и тот факт, что перед каждым детектором находится стандартный рассеиватель (металлический ванадий), с помощью которого во время измерения образца регулярно производится абсолютная калибровка сечения рассеяния с систематической погрешностью не более 10%. Оказалось, что для слаборассеивающих образцов (сечение рассеяния меньше $10 \mbox{ см}^{-1}$) не требуется дополнительного измерения пропускания образца [8]. Это дает возможность параллельно измерениям проводить первичную обработку экспериментальных данных сразу в абсолютной шкале интенсивностей.

Потоки тепловых нейтронов на образце чрезвычайно велики [9], а мертвые времена пропорциональных $He^3$-детекторов -- микросекунды, следовательно, необходима коррекция на мертвые времена [10].

Кроме того, использование времени пролета приводит к некоторой избыточности данных. Дело в том, что для заданного интервала переданных импульсов данные с разных колец (детекторов) будут иметь одно и то же значение для разных длин волн:

$$\begin{eqnarray*} q = \frac{4\pi \sin (\Theta /2) }{\lambda} , \end{eqnarray*}$$

где $\Theta$ -- угол рассеяния, $\lambda$ -- длина волны нейтрона. Поэтому одним из центральных моментов является усреднение данных. Экспериментатор задает интервал по $q$ и количество точек в усредненном спектре. При этом может оказаться, что в некоторые отрезки разбиения этого интервала попадает несколько точек от разных колец.

Очень часто два понятия -- дифракция и малоугловое рассеяние -- смешивают по причине очень близких физических процессов. Действительно, и в том, и в другом случае речь идет о когерентном и упругом рассеянии нейтронов. Но отличие в том, что дифракция -- это рассеяние на периодической структуре, а малоугловое рассеяние -- на структуре, не имеющей периодичности. Поэтому, иногда употребляют термин диффузное рассеяние. Конечно, существуют и периодические структуры с большими параметрами решетки, и тогда тоже возникает дифракционное рассеяние нейтронов на общей картине диффузного рассеяния в малоугловой области.

Существует несколько типов взаимодействий тепловых нейтронов с веществом. Основную роль играют ядерное (взаимодействие с ядрами) и магнитное (взаимодействие между магнитными моментами нейтрона и атома). Каждое из взаимодействий проявляется в экспериментах по рассеянию как некоторое сечение рассеяния. Ядерное и магнитное рассеяние может быть когерентным и некогерентным, упругим и неупругим. В малоугловом рассеянии интересуются когерентной и упругой составляющей. Другие компоненты рассеяния (некогерентное и неупругое), разумеется, тоже присутствуют в рассеянии, однако должны быть вычтены.

Таким образом, из всего рассеяния нас интересует только когерентное и упругое. Практически это означает необходимость устранения не только факторов, связанных, например, с потоками нейтронов, эффективностью детекторов, но и некогерентной и неупругой составляющей. Кроме того, отсутствие нейтроновода не только повышает поток нейтронов на образце, но и создает высокий инструментальный фон, который тоже должен быть устранен из спектра рассеянных нейтронов. Для решения этих задач используется фоновый образец, подготовленный таким образом, чтобы выделить в чистом виде когерентную и упругую составляющие рассеяния. Это делается путем вычитания из спектра образца фонового спектра.

Для сильно рассеивающих образцов (сечение рассеяния свыше $10 \mbox{ см}^{-1}$) стандартная процедура уже не дает требуемой точности и, следовательно, должна быть иной. В этом случае необходимо провести дополнительное измерение так называемого пустого пучка, т.е. измерение при отсутствии образца.

Времяпролетный метод

Исследования методом малоуглового рассеяния нейтронов (МУРН) проводятся на реакторах (условно называемых ``стационарными''), а также на ускорителях. Импульсный реактор ИБР-2 сочетает в себе достоинства стационарных реакторов (высокий поток в первую очередь) и периодический характер мощности, как это реализуется на ускорителях. Поэтому можно организовать нейтронный эксперимент существенно иначе, чем на стационарных реакторах, где из энергетического спектра тепловых нейтронов (максвеловское распределение) вырезается узкая часть выбранной длины волны. Отрезание производится с помощью либо волнового селектора, либо совершенного кристалла.

Только применение времяпролетного метода (ВПМ) позволяет использовать все возможности подобного реактора. Поскольку скорость тепловых нейтронов невелика, есть возможность осуществить анализ длины волны нейтрона по времени пролета. Это привело к созданию нейтронных спектрометров по времени пролета (английский термин Time-Of-Flight -- TOF): нейтроны от импульсного источника после замедления до тепловых энергий пролетают до образца, затем рассеиваются на образце и регистрируются детектором. Зная расстояние, которое пролетел нейтрон, и время от импульса (вспышки, старта) реактора, можно определить длину волны зарегистрированного нейтрона, используя формулу

$$\begin{eqnarray*} \lambda=\frac{ht}{mL} , \end{eqnarray*}$$

где $\lambda$ -- длина волны, $h$ -- постоянная Планка, $t$ -- время пролета, $m$ -- масса нейтрона, $L$ -- пролетная база. Для длин волн, измеряемых в ангстремах, времени -- в милисекундах, а расстояний -- в метрах, получим

$$\begin{eqnarray*} \lambda=3.958\frac{t}{L} . \end{eqnarray*}$$

Диапазон используемых на TOF-спектрометре длин волн может быть очень широким (на ЮМО это 0.07 nm - 0.8 nm). Это позволяет получить большой динамический диапазон по переданному импульсу при весьма скромных размерах детекторов. ВПМ-метод позволяет с высокой точностью (определяемой шириной вспышки) определить длину волны нейтрона. Высокое разрешение по длине волны недостижимо, например, с помощью волнового селектора.

Краткое описание установки

Рис.: Установка малоуглового рассеяния нейтронов ЮМО (4-й канал ИБР-2): 1 - отражатели, 2 - зона реактора с замедлителем, 3 - прерыватель, 4 - сменный коллиматор, 5 - вакуумная труба, 6 - юстируемый коллиматор, 7 - термостат, 8 - кассета с образцами, 9 - стол образцов, 10 - ванадиевый стандарт, 11, 12 - детекторы (``OLD'' и ``NEW'' соответственно), 13 - детектор прямого пучка

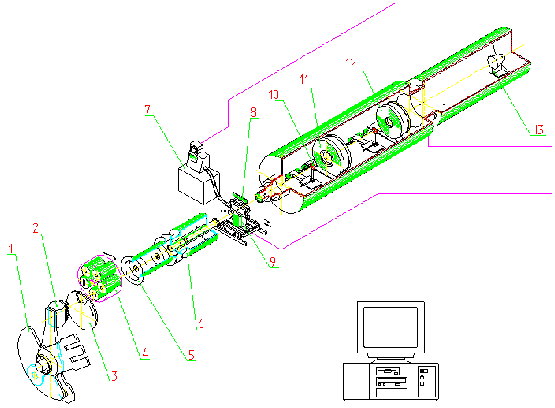На рис.1 приведена схема малоуглового спектрометра ЮМО. Нейтроны, возникшие в результате прохождения рефлекторов 1 вблизи зоны 2, термализуются в замедлителе. Сформированный коллимационной системой 4-5 пучок нейтронов попадает на образец 8, где рассеивается и приходит на детекторы 11, 12 и 13. Более подробное описание работы спектрометра в двухдетекторном варианте можно найти в [3].

Процедура измерений и соответствующие формулы

Рассмотрим элемент объема $dx\,dy\,dz$, находящийся на расстоянии $x$ по направлению оси нейтронов, падающих на образец толщиной $d$. Интенсивность нейтронов, рассеянных в телесный угол $\Omega$ будет

$$i = I_0(y,z)\, \eta(x,y,z)\, \frac{d\sigma}{d\Omega}\, \Omega\, \epsi... ... T_{1}(x,y,z)\, T_{2}\left(\frac{d-x}{\cos\Theta},y,z\right)\, dx\, dy\, dz\, ,$$ (1)

где $I_0(y,z)$ -- поток нейтронов на образце, $\eta(x,y,z)$ -- количество рассеивающих частиц в единице объема образца, $\frac{d\sigma}{d\Omega}$ -- дифференциальное сечение рассеяния (включая некогерентную часть), $T_{1}$ и $T_{2}$ -- пропускание образца до элемента объема $dx\,dy\,dz$ и после соответственно, $\epsilon$ -- эффективность детектора, $\Theta$ -- угол рассеяния.

В случае малых углов произведение $T_{1}$ и $T_{2}$ будет функцией только толщины. Для тонкого гомогенного образца и изотропного в пределах образца пучка уравнение для единичной площади образца будет выглядеть как

$$I = \int\limits_{0}^{d} I_0\, \frac{d\Sigma}{d\Omega}\, \Omega\, \epsilon\, T(x)\, dx\, .$$ (2)

В результате, получим :

$$I = I_0(\lambda)\, \frac{d\Sigma}{d\Omega}\, \Omega\, \epsilon(\lambda)\, T(d)\, .$$ (3)

Стандартная процедура измерения

на малоугловой установке ЮМО (см. [3]) включает в себя измерение образца:

$$I_{s} = I_0(\lambda)\, \epsilon(\lambda)\, T_{s}\, \left(\frac{d\Sigma}{d\Omega}\right)_{s}\, \Omega_{s}\, d_{s}\, ,$$ (4)

и измерение образца с ванадием одновременно:

$$I_{s+v} = I_{s} + I_0(\lambda)\, \epsilon(\lambda)\, T_v\, T_{s}\, \left(\frac{d\Sigma}{d\Omega}\right)_{v} \Omega_{v}\, d_{v}\, ,$$ (5)

где $I_{s}$ и $I_{s+v}$ -- интенсивности на детекторе, $I_0(\lambda)$ -- интенсивность нейтронного пучка на образце, $\epsilon(\lambda)$ -- эффективность детектора, $T_v$ -- пропускание ванадиевого рассеивателя, $d_{v}$ -- толщина ванадиевого стандарта, $\left(d\Sigma/d\Omega\right)_{v}$ -- дифференциальное сечение рассеяния ванадиевого стандрата. Эти короткие измерения, чередуясь, повторяются для того, чтобы исключить влияние долговременных колебаний мощности реактора в процессе эксперимента. Из комбинации (4) и (5) можно получить

$$\frac{\left(d\Sigma/d\Omega\right)_{s}}{\left(d\Sigma/d\Omega\right)_{v}} = \frac{I_{s}}{I_{s+v}-I_{s}} \frac{T_v\Omega_{v}d_{v}}{\Omega_{s}d_{s}} .$$ (6)

Из уравнения (6) следует, что, дополнительный эксперимент для измерения пропускания образца не нужен. Полученный результат устойчив к долговременным колебаниям мощности, и можно проводить обработку данных непосредственно в процессе эксперимента.

Нестандартная процедура измерения

подразумевает следующее. Из уравнения (6) следует, что ошибка отношения интенсивностей образца и ванадия чувствительна к разнице в интенсивностях ванадия и образца. Если образец имеет большое сечение рассеяния, ошибка в интенсивности увеличивается. Это требует увеличения времени экспозиции с ванадием и образцом по отношению ко времени экспозиции образца. Для того, чтобы не увеличивать время экспозиции на спектрометре ЮМО, существует альтернативная процедура измерения, когда производится дополнительное измерение так называемого пустого пучка, т.е. измерение фона и только ванадиевого стандарта перед детектором. К уравнениям, описанным в предыдущем параграфе, добавятся уравнения от ванадиевого стандарта при отсутствии образца (измерения пустого пучка).

Формулы же для образцов с сильным рассеянием подобны формуле 4:

$$I_{s} = I_0(\lambda)\, \epsilon(\lambda)\, T_{s}\, \left(\frac{d\Sigma}{d\Omega}\right)_{s}\, \Omega_{s}\, d_{s}\, .$$ (7)

Но затем проводится измерение пустого пучка, когда рассеивает только ванадиевый стандарт, находящийся перед детектором непосредственно:

$$I_{v} = I_0(\lambda)\, \epsilon(\lambda)\, T_{v}\, \left(\frac{d\Sigma}{d\Omega}\right)_{v}\, \Omega_{v}\, d_{v}\, ,$$ (8)

где $I_{v}$ -- интенсивность на детекторе от образца, $I_0$ -- поток на образце, $\epsilon(\lambda)$ -- эффективность детектора, $\left(d\Sigma/d\Omega\right)_{v}$ -- дифференциальное сечение рассеяния образца, $d_{v}$ -- толщина ванадия, $\Omega_{v}$ -- телесный угол образуемый из позиции ванадиевого стандарта до детектора. В результате нормированное дифференциальное сечение будет

$$\frac{\left(d\Sigma/d\Omega\right)_{s}}{\left(d\Sigma/d\Omega\right)_{v}} = \frac{I_{s}}{I_{v}}\, \frac{T_{s}}{T_{v}}\, \frac{d_{v}}{d_{s}}\, \frac{\Omega_{v}}{\Omega_{s}}\, .$$ (9)

В (9) присутствует дополнительный сомножитель -- пропускание образца. Для определения пропускания можно воспользоваться данными от детектора прямого пучка. Формулы для детектора прямого пучка будут выглядеть как

$$I^{d}_{s} = I\, \epsilon^{d}\, T_{s}\, , \quad I^{d}_{e} = I\, \epsilon^{d} ,$$ (10)

где $I^{d}_{s}$ -- интенсивность на детекторе прямого пучка для образца и $I^{d}_{e}$ -- интенсивность на детекторе прямого пучка для случая отсутствия образца, $I$ -- поток на образце, $\epsilon^{d}$ -- эффективность детектора прямого пучка, $T_{s}$ -- пропускание образца.

Подставляя отношение интенсивностей от образца, полученное на детекторе прямого пучка, из уравнений (10) в (9) получим:

$$\frac{\left(d\Sigma/d\Omega\right)_{s}}{\left(d\Sigma/d\Omega\right)_{v}} = \frac{I_{s}}{I_{v}}\, \frac{1}{T_{v}}\, \frac{I^{d}_{s}}{I^{d}_{e}}\, \frac{d_{v}}{d_{s}}\, \frac{\Omega_{v}}{\Omega_{s}}\, .$$ (11)

Уравнение (11) содержит только константы и измеренные интенсивности. Все представленные формулы не содержат фоновой составляющей. Этот вопрос должен быть рассмотрен отдельно.