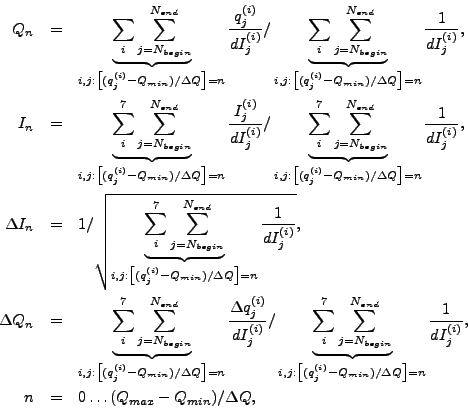


Next: Используемые параметры
Up: The Sas Handbook
Previous: Введение
Contents
Subsections
Спектр каждого кольца детектора корректируется следующим образом.
Вносятся поправки на мертвые времена детекторов:
где
 -- количество стартов реактора (длительность экспозиции),
-- количество стартов реактора (длительность экспозиции),
 -- мертвое время детектора,
-- мертвое время детектора,
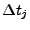 -- ширина
-- ширина 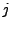 -го временного канала.
-го временного канала.
Спектры нормируются на ширины временных каналов:
(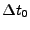 -- ширина нулевого временного канала).
-- ширина нулевого временного канала).
Из ненулевых каналов каждого спектра вычитается фон тепловых нейтронов,
вычисленный с учетом параметров реактора и установки, и при определенных
условиях, -- фон быстрых нейтронов (константа):
Нормировка спектров на рассеяние ванадиевого стандарта производится следующим
образом:
где
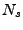 и
и 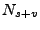 -- количество стартов реактора,
-- количество стартов реактора,
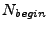 и
и 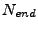 -- заданные начальный и конечный каналы для
обработки (остальные каналы зануляются),
а множитель
-- заданные начальный и конечный каналы для
обработки (остальные каналы зануляются),
а множитель 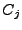 вычисляется с учетом параметров детектора.
вычисляется с учетом параметров детектора.
После этого из спектра каждого кольца детектора вычитаются имеющиеся фоновые
спектры (растворитель, кювета), и спектр нормируется на толщину образца:
где
множитель 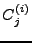 вычисляется как при стандартной процедуре нормировки,
вычисляется как при стандартной процедуре нормировки,
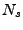 и
и 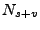 -- количество стартов реактора,
-- количество стартов реактора,
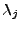 -- длина волны нейтрона,
а коэффициенты
-- длина волны нейтрона,
а коэффициенты 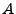 и
и 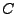 вычисляются в зависимости от выбранной модели
пропускания (используются или нет данные ``пустого пучка'').
вычисляются в зависимости от выбранной модели
пропускания (используются или нет данные ``пустого пучка'').
Полученный спектр нормируется на толщину образца:
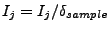 .
.
где
множитель 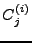 вычисляется, как при стандартной процедуре нормировки,
а нормировочные множители вычисляются следующим образом:
вычисляется, как при стандартной процедуре нормировки,
а нормировочные множители вычисляются следующим образом:
где
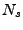 и
и 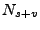 -- количество стартов реактора,
-- количество стартов реактора,
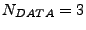 , если используются данные кюветы, и
, если используются данные кюветы, и
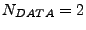 -- если не используются.
-- если не используются.
Полученный спектр нормируется на толщину образца:
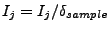 .
.
Производится переход в Q-пространство (Q - переданный импульс нейтрона).
Значения переданного импульса нейтрона и его дисперсии вычисляются по
формулам:
где
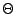 и
и 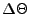 -- средний угол рассеяния для соответствующего
детектора рассеяния и его дисперсия,
-- средний угол рассеяния для соответствующего
детектора рассеяния и его дисперсия,
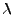 -- длина волны нейтрона,
-- длина волны нейтрона,
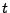 и
и 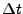 -- середина временного канала и его ширина.
Средний угол рассеяния и его дисперсия вычисляются по формулам
-- середина временного канала и его ширина.
Средний угол рассеяния и его дисперсия вычисляются по формулам
где 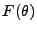 -- функция разрешения установки,
-- функция разрешения установки,
Усреднение на интервале
![$[Q_{min},Q_{max}]$](img87.gif) с шагом
с шагом 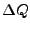 производится
следующим образом:
производится
следующим образом:
суммирование производится для ненулевых значений
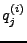 ,
, ![$I^{(i)}[j]$](img91.gif) и
и ![$ dI^{(i)}[j]$](img92.gif) ,
верхний индекс обозначает номер кольца детектора.
Возможно исключение некоторых колец из процедуры усреднения.
,
верхний индекс обозначает номер кольца детектора.
Возможно исключение некоторых колец из процедуры усреднения.
В программе предусмотрена возможность отказа от усреднения --
в этом случае производится сортировка точек спектра по величине
переданного импульса нейтрона.
Alexei Soloviev
2008-09-14
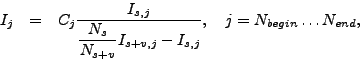
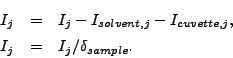
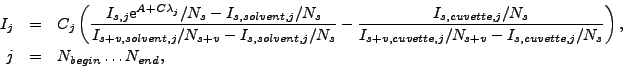
![]() .
.
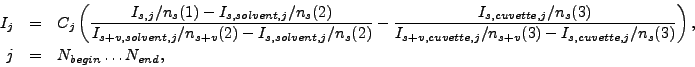

![]() .
.
![\begin{eqnarray*}
q =
\frac{4\pi \sin (\Theta /2) }{\lambda} \approx
\frac{2\pi...
...^2} +
\frac{1}{12} \left(\frac{\Delta t}{t}\right)^2 \right] ,
\end{eqnarray*}](img81.gif)
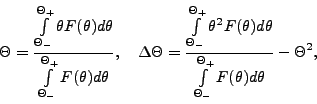
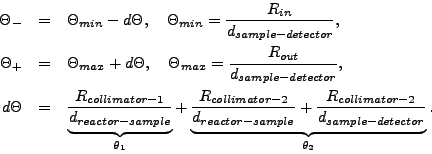
![]() с шагом
с шагом ![]() производится
следующим образом:
производится
следующим образом: